In our previous post we explained how to determine the strength of a transverse fillet weld. A transverse fillet weld is one that is perpendicular to an applied load. We will now look at how to determine the strength of a fillet weld under shear stress.
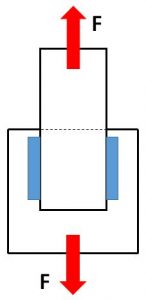
If the load applied is not perfectly perpendicular to the fillet weld, the weld is in shear and its load carrying capacity is greatly reduced. Because of this reason, when designing welds we always assume that the weld will be loaded in shear as seen below.
In this case the applied load is parallel to the welds. The forces are pulling the members being joined in opposite directions, which places the welds under shear. When a weld is in shear we cannot longer use the tensile strength of the filler metal to determine the strength of the weld. Instead, the tensile strength is reduced by a factor in order to assure safety. Clause 2 of AWS D1.1 requires that the minimum tensile strength of the filler metal be multiplied by 0.30 to obtain the allowable shear stress on the weld.
The calculation is the exact same as when calculating the strength of a transverse fillet weld, except for the safety factor. The notation now shows the maximum shear stress (τ) allowed rather than the maximum tensile stress (σ).
Where,
is the maximum allowed shear stress on the weld
F is the force the weld can handle, in other words, the strength of the weld in lbf
A is the effective area of the weld
Notice that instead of (tensile stress) we now have (allowable shear stress).
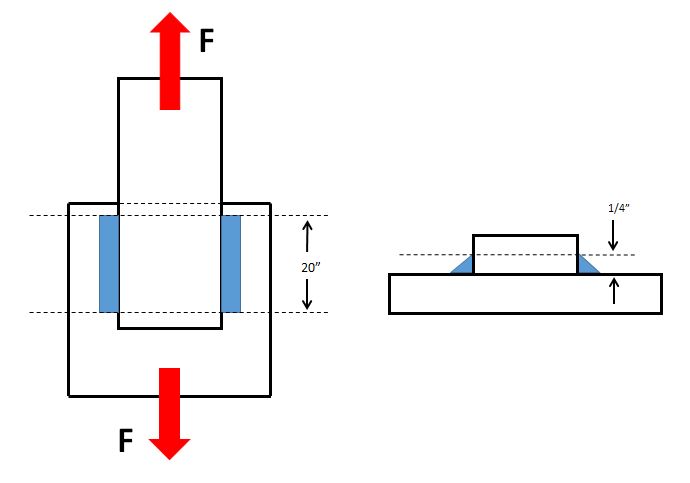
For our example we will use the same numbers we used on our previous post for determining the strength of a transverse fillet weld. We are using an ER70S-6 filler metal with minimum tensile strength of 70,000 psi. We are placing two (2) 20-inch long lap welds on both sides of the joint.
The allowable shear stress for the welds would be 70,000 psi x 0.30 = 21,000 psi. A reduction of 70% compared to the case where the fillet weld was in pure tension.
If our two welds are ¼-inch fillets then the shear strength (load carrying capacity) of the welds is calculated as follows.
First, we rearrange the formula provided above to solve for F.
We already know that the allowable shear stress is 70,000 x 0.30 = 21,000 psi. To get A (effective area of the weld) we need
to multiply the theoretical throat size (1/4 x 0.707 = 0.177 inches) times the length (20 inches) times 2 welds.
The effective area equals 20in x 0.177in x 2 = 7.08 sq-in.
We can now solve for F.
F = 21,000 x 7.08 = 148,680 lbf
Because the welds were placed parallel to the applied load, the allowable force is 70% less than if we had placed the welds perpendicular to the applied load (as in the example on the previous post).
Understanding how loads act upon weldments is not easy, even for accomplished welding engineers and design engineers. But having this knowledge can improve structural integrity and reduce costs by reducing the amount of weld.

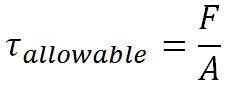


Explained perfectly.
thank you, this is interesting stuff. I am new to the fuels industry as an estimator. I enjoy math and learning. One question, where does the .707 come from? (the number used to multiply with the throat size).
It’s using trigonometry to calculate the dimension of the throat. Cos 45 = (throat/leg size)
0.707 = throat x leg size
Since you can measure the leg size the throat is the only missing variable and can be calculated.
I am a women welder and I confuse it with Fillet welding so explain what is fillet welding.
Fillet welding is not a correct term. However, it refers to the making of filled welds. Fillet welds are made in both tee and lap joints.
When using the allowable shear (30%) for welds…is there already a safety factor built into this calculation (if so do we know it?) or is this a limit, for which we need to add additional safety factors too.
Thanks for your help
There is a factor of safety in using this calculation from the design clause of AWS D1.1. The code even allows you to use up to 45% of minimum specified tensile strength if the direction of loading is perpendicular to the axis of the weld. But even in this case, there is a factor of safety.
Can anyone advise: when calculating shear stress of a welded tee section with a fillet weld down both sides, what do you assume for weld length? Do you count each weld and therefore it is 2 x the weld run?
Yes, you are correct. You are calculating total weld effective area. So if you have a 10-inch long weld on both side your total length for the calculation would be 20 inches. The example in this post shows this by multiplying by a factor of two.
Thanks for the articles – i’ve been reading them with great interest.
I have a question that I hope you have time to help me with. There just some basics that I don’t know enough about. I will do my best to explain the problem in the absence of pictures.
I’m trying to calculate the load capacity of a steel stand, where one side is fully supported by vertical steel legs, but the other side of the horizontal load-carrying-surface is fillet-welded to 5 vertical steem beams.
So in other words – one side is supported, and the other side is depending on the welds.
So the calculation is the load carrying capacity of the 5 identical fillet welds.
Material is square steel tubing, with measurement (metric in mm 30x30x3) approximately 1,2″x1,2″ and material thickness of 1/8″
The fillet welds are each no less than 3 inches long, I believe the welds are 3/16″, so throat would be 0.133. Effective area for the 5 welds combined would be approximately 2 sq-in
I’m can’t be sure which wire was used to weld. Is it safe to assume a wire of 70.000 PSI multiplied by 0.30 to get shear stress?
In my calculations I get that the 5 fillet welds will have a combined load carrying capacity of around 40000 lb. (and I need it to carry 4-5000lb, so I guess I should be home free?)
Thanks in advance for any insight you can give on this problem.
Great question. As you stated, 5 welds with throats measuring 0.133 would have an effective area of (0.133) x (5 welds) x (3in) = 1.995 sq-in. The allowable shear stress would be 1.995 x 70,000psi x 0.30 = 41,895 lbf.
This has the safety factor built into it by using the calculations provided by AWS D1.1. Without a drawing which can be used to verify the distribution of loads I could not guarantee this is acceptable. However, more than likely it is, just as you stated.
Things that can affect this are:
1. Is this static loading? If so you should be OK.
2. Is it cyclically loaded? You would need to look at the stress range. Or, if it is loaded with impact – let’s say a 10,000 lb load is dropped on it then you must consider acceleration. Remember, Force = mass x acceleration.
3. Welding discontinuities – cracks, undercut, overlap and other discontinuities can act as stress risers and increased the stress generated by the load.
4. Location of welds. If the weld is placed on the top surface of the tubing connected to the beam then the root of the weld will be in tension – which is not desirable. If you can place an additional weld on the bottom this takes care of that problem, as the bottom weld would have the root in compression and the face in tension.
If you ever get a diagram we can take a closer look.
Good luck!
Wow, I can’t tell you how much I appreciate you taking the time to reply to my problem. Really has given me peace of mind.
The steel stand will be carrying a big fish tank, so static load indeed. And all the welds look good.
The welds are located on the bottom and both sides of where the tubing connect to the beams. So guess that should be ok as well. 🙂
Thanks again for your help.
Very helpful thank you. I am doing some calculations on weld connections to prove that a weld is strong enough. The connection is a pipe connecting to a flat plate. Is this something that I could use this shear force calculation on?
Yes. It would be the same since it is also a fillet weld. If following D1.1 then the maximum allowable stress on that welds remains 0.30 x minimum tensile strength of the filler metal.
I want to know the factor of safety for fillet weld.
That would depend on the size of the fillet weld. You can design a weld to give you only the strength that is required to carry the load imposed on it. If the weld must be 3/16″ and you go with 1/4″ you will have a different safety factor than if you go with a 5/16″ fillet weld. The safety factor is determined by the design engineer that determines the weld sizes.
Thank you, i need some knowledge on weld connections in structures.
What kind of information are you looking for? We get involved with welded connection design quite often. Anything specific you would like to know about?